To compare concurrent Algorithms, a problem called Dining Philosophers comes in handy. The problem helps us explore important concepts like deadlocks and fairness. Edsger Dijkstra introduced it to the Computer Science community in 1965. We will look at the problem in detail, discuss its challenges, and explore several solutions. For each solution, we evaluate algorithms according to their capabilities in addressing concurrency challenges. This website features a Java-based Simulation and Animation page that will let you experiment with the discussed concepts.
The Dining Philosophers Problem
The Philosophers
We will use the following definition: Philosophers sit around a table with a chopstick between each pair. They begin by thinking, then attempt to pick up the chopsticks on their left and right. Only one philosopher can hold a chopstick at a time, so they may need to wait until their neighbor returns it to the table. If two philosophers try to pick up the same chopstick simultaneously, only one will succeed. Once a philosopher has acquired both chopsticks, they may eat. After eating, they return the chopsticks, and the cycle repeats.
The naive process of a philosopher consists of:
- Think for some time (independent process action)
- Pick up left Chopstick or wait until available
- Pick up right Chopstick or wait until available
- Eat for some time (process action that needs exclusive access to shared resources)
- Put down left chopstick and notify availability
- Put down right chopstick and notify availability
This cycle runs for all philosophers simultaneously. In our case, we want the process to run until a specified timeout is reached. When this time limit is reached, all philosophers are terminated. Note that the Dining Philosophers problem can be formulated in several ways, and this is just one of them.

To keep track of the philosophers' actions, we keep a Log for each philosopher, tracking the following Events:
- [ T ] = Think
- [PUL] = Pick Up Left
- [PUR] = Pick Up Right
- [ E ] = Eat
- [PDL] = Put Down Left
- [PDR] = Put Down Right
- [ B ] = Blocked (Whenever waiting for a Chopstick occurs)
Whenever philosophers complete an action, they will add it to their log. The combination of all the philosophers' logs will result in a timeline, in which we are able to track the actions of the philosophers over the course of the simulation. To keep the timeline consistent, we use a virtual clock, which is used by the philosophers to log their actions according to simulation time.
Here is an example for a timeline that we get as a result of a simulation:
Scroll -------->
PH_0 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ ][ ][PUL][PUR][ E ][ ][ E ][ E ][ E ][ E ][ E ][PDL][PDR][ ][ ][ ][ ][ ][ ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ B ][ ][ ][PUL][ ][ ][ ][PUR][ ][ E ][ E ][ E ][ E ][ E ][ E ][ E ][ ][ ][ ][ E ][ E ][PDL][PDR][ ][ ][ ][ T ][ T ][ T ][ T ][ T ][ T ][ ][ ][ ][ ][ T ][ ][ ][ ][ T ][ T ][PUL][ B ][ B ][ B ][ ][ ][PUR][ ]
PH_1 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ ][ ][ ][ ][ T ][ ][ B ][ B ][ B ][ B ][ B ][ ][ ][PUL][ ][ ][PUR][ ][ ][ E ][ E ][ E ][ E ][ E ][ E ][ E ][ E ][ E ][ ][ ][ ][ ][PDL][PDR][ ][ ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ ][ ][ ][ T ][ T ][ ][ ][ ][ ][PUL][ B ][ B ][ B ][ B ][ B ][ B ][ ][ ][ ][PUR][ E ][ ][ ][ ][ E ][ E ][ ][ E ][ E ][ E ][PDL][PDR][ ][ ]
PH_2 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][PUL][PUR][ ][ ][ E ][ ][ E ][ E ][ E ][ E ][ E ][ ][ ][ ][ ][PDL][ ][PDR][ ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ B ][ ][ ][ ][ ][ ][ ][ ][PUL][ B ][ B ][ B ][ B ][ B ][ B ][ B ][ ][ ][PUR][ E ][ E ][ ][ ][ ][ ][ ][ E ][ E ][ E ][ E ][ E ][ E ][PDL][PDR][ ][ ][ T ][ ][ ][ ][ T ][ T ][ ][ T ][ T ][ T ][ ][ ][ ][PUL]
PH_3 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ ][ ][ ][ ][ T ][ ][ T ][ T ][ B ][ B ][ B ][ ][ ][ ][ ][ ][ ][ ][PUL][ B ][ B ][ B ][ B ][ B ][ B ][ B ][ B ][ B ][ ][ ][ ][PUR][ ][ ][ ][ ][ E ][ E ][ E ][ E ][ E ][ E ][ E ][PDL][PDR][ ][ T ][ T ][ ][ ][ ][ ][ ][ T ][ T ][ T ][ T ][ T ][ B ][ ][ ][PUL][ ][ B ][ ][ ][PUR][ E ][ E ][ ][ E ][ E ][ E ][ ][ ][ ][ ]
PH_4 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ ][ ][ ][ ][ T ][PUL][ B ][ B ][ B ][ B ][ B ][ ][ ][ ][PUR][ ][ ][ ][ ][ E ][ E ][ E ][ E ][ E ][ E ][ E ][ E ][ E ][PDL][PDR][ ][ ][ ][ ][ ][ ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ ][ ][ ][ T ][ T ][ ][ ][PUL][PUR][ ][ E ][ E ][ E ][ E ][ E ][ E ][ ][ ][ ][ ][ E ][PDL][PDR][ ][ T ][ T ][ ][ T ][ T ][ T ][ ][ ][ ][ ]
TIME: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84
Scroll -------->
Note that whenever a philosopher attempts to pick up or put down a chopstick, we assume a synchronization point to determine the correct order of these actions after the simulation. Empty brackets are displayed to signify that philosophers took no action at that time.
We determine the time spent eating and thinking using the following distributions:
- Deterministic: The time-delay for eating or thinking is the same for all philosophers.
- Interval: The time-delay is randomly selected within a specific range, for example, between 50 and 100 milliseconds.
- Normal: The time-delay varies symmetrically around a mean, with deviations following a normal distribution.
- Exponential: The time-delay is usually small, but occasionally, much larger values can occur, following an exponential distribution.
Challenges
There are three main challenges we encounter in the Dining Philosophers problem: Deadlocks, starvation/fairness and concurrency. We also introduce two "side challenges": implementation and performance. The effectiveness of our solution in addressing one or more of these challenges will help us evaluate the quality of the different approaches later on.
Deadlocks
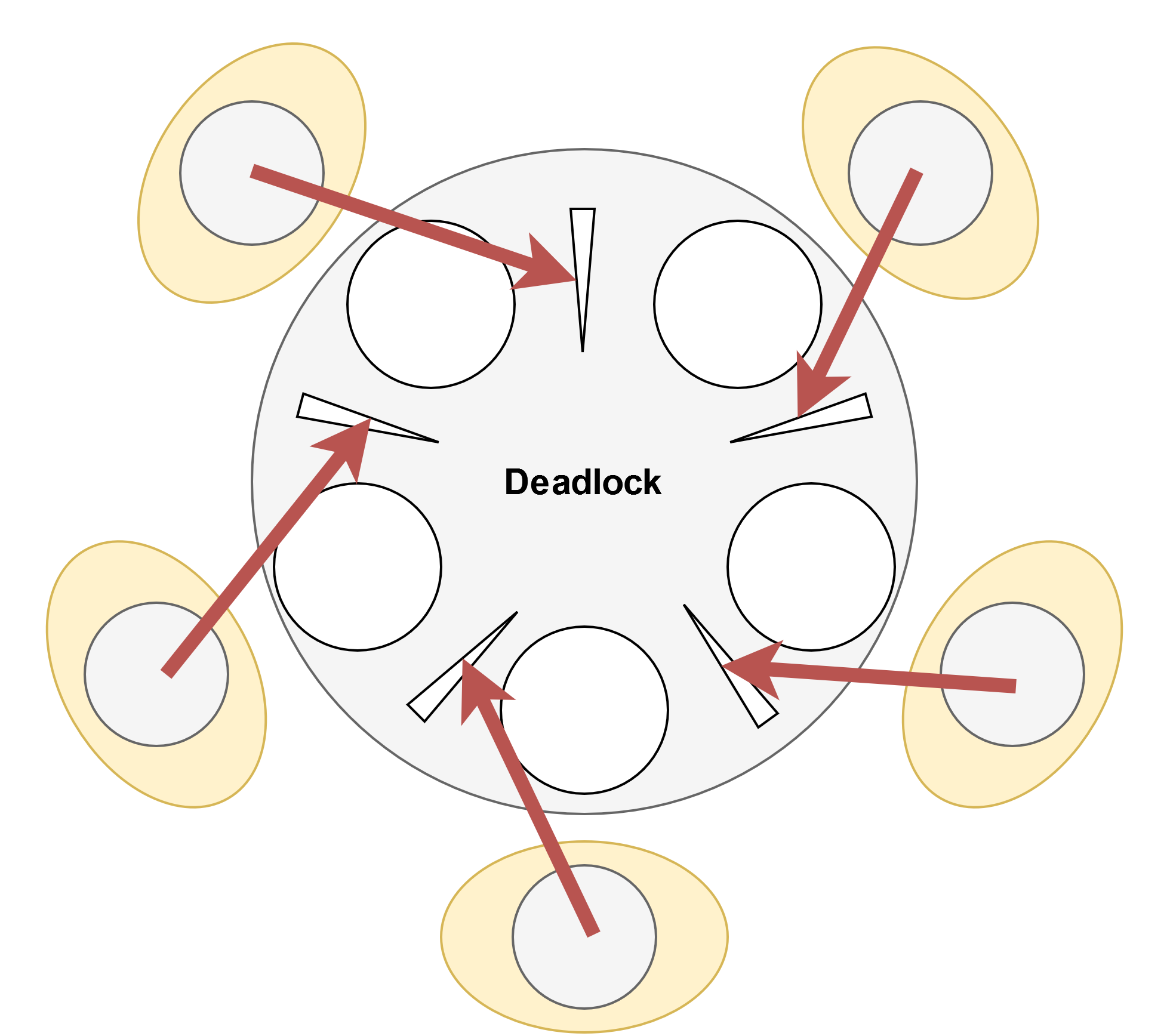
Deadlocks can occur if all the philosophers pick up the chopstick to their left simultaneously and then wait for the chopstick to their right. In this situation, none of the philosophers can proceed, leading to indefinite waiting. This occurs because the system satisfies the Deadlock conditions, as defined by Coffman: mutual exclusion (each chopstick can only be held by one philosopher), hold and wait (philosophers hold one chopstick while waiting for another), no preemption (the pick-up is not interrupted), and circular wait (each philosopher is waiting for a chopstick held by the philosopher next to them). Preventing deadlocks by addressing these conditions is the primary goal of the solutions we aim to explore.
Here is an example of a Simulation that resulted in a deadlock:
PH_0 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ ][ ][ ][ ][PUL]
PH_1 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ B ][ ][PUL][ ][ ][ ]
PH_2 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ B ][ B ][ ][ ][PUL][ ][ ]
PH_3 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ T ][ B ][PUL][ ][ ][ ][ ]
PH_4 [ T ][ T ][ T ][ T ][ T ][ T ][ T ][ B ][ B ][ ][ ][ ][PUL][ ]
TIME: 1 2 3 4 5 6 7 8 9 10 11 12 13 14
For convenience, we assume that philosophers usually pick up their left chopsticks first; thus, we can conveniently track whether a deadlock has occurred by checking if the last action of all philosophers was a [PUL] = Pick Up Left.
At this stage, it is useful to introduce the concept of "precedence graphs", which are used to represent dependencies between tasks. In the context of the Dining Philosophers problem, each philosopher is represented as a node, and the directed arrows indicate the dependency of having to wait for a chopstick. Since all philosophers have to wait for their right neighbor, this means that there is a circular dependency of the philosophers.
Cyclic dependencies like these indicate potential deadlocks in a system (essentially a visualization of the circular-wait condition). Avoiding this circular pattern is one of the main ways we are going to prevent deadlocks in a Dining Philosophers solution. Another crucial detail is the length of the precedence path, as it is at the maximum length in the naive approach. Long paths in a precedence graph mean that there are potentially long waiting chains that harm parallelism.
Starvation and Fairness
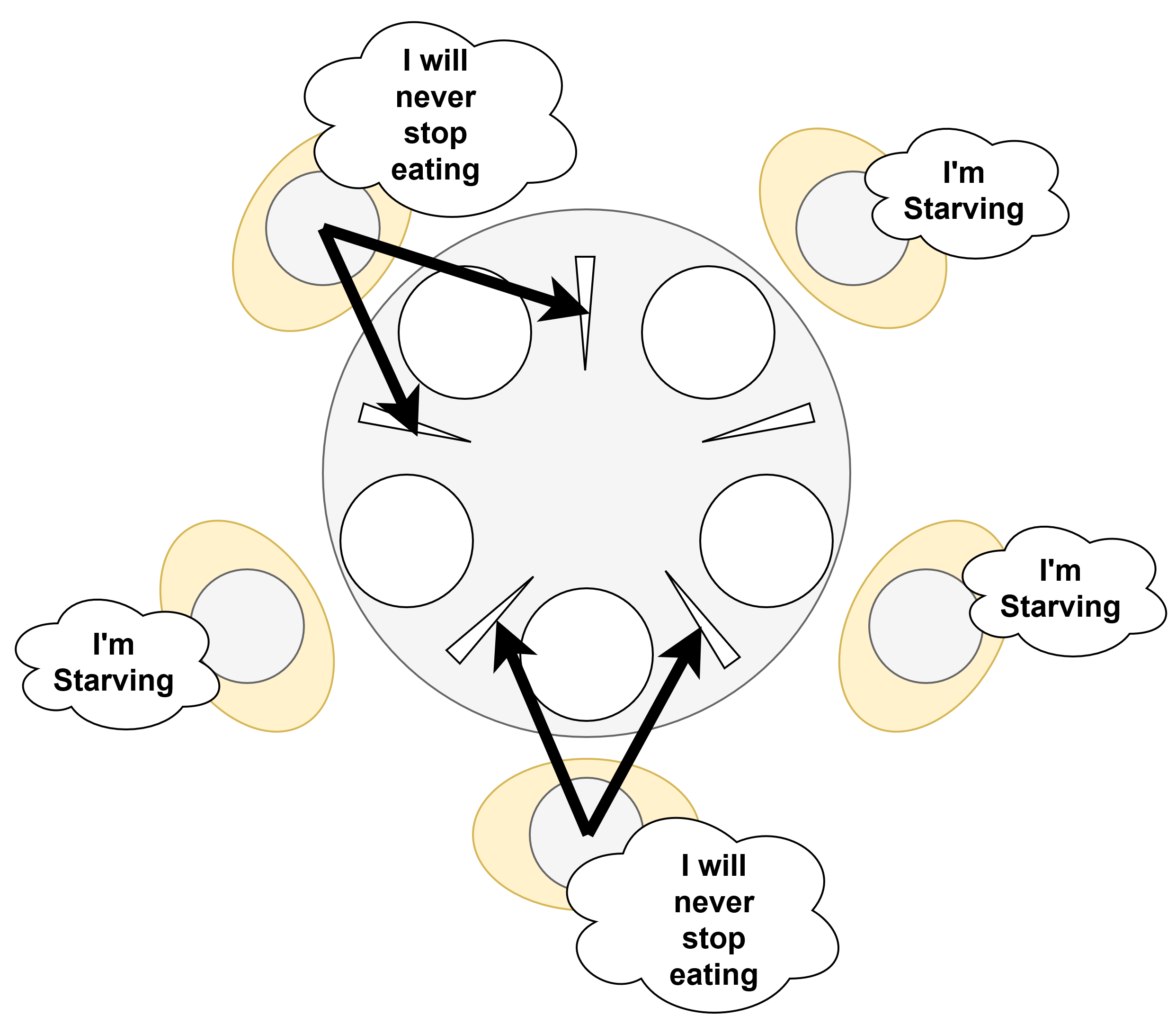
Starvation happens when a philosophers rarely, or never, get a chance to eat. The prime example of starvation is deadlocks, which starve all philosophers. Other examples of starvation are: One philosopher repeatedly grabs the chopstick first, stopping a neighbor from eating. One philosopher takes a very long time to eat, making neighbors wait for access to the chopstick. The goal is to make sure that every philosopher has a fair chance to eat (and not starve), we call this fairness. There are several ways in which starvation and fairness can be defined for the Dining Philosophers problem. In the following, we want to consider starvation as the theoretical possibility of philosophers not being able to eat at all after a certain point in time. Thus, if there is no starvation in our system, philosophers who want to pick up chopsticks will eventually succeed. With this definition, we guarantee fairness whenever a system is starvation-free. With our solution, we aim to prevent deadlocks while also maintaining fairness as much as possible.
Additional to the basic notion of fairness of eventually succeeding to pick up, we introduce the two measures:
- Eat Chance Fairness: We count how often each philosopher eats and calculate the standard deviation across all philosophers chances to eat(variation from the average). Large values mean bad fairness, while values near zero indicate good fairness.
- Eat Time Fairness: We also track the total simulation time each philosopher spent eating and calculate the standard deviation across all philosophers' eating times. Large values again mean bad fairness, while small values mean good fairness. This measure depends heavily on the chosen distribution — for example, the exponential distribution might return large outliers.
In the context of implementations, we sadly have to accept that scheduling of threads (and consequently philosophers) is never fair. The Operating system and in the case of Java, the Java Virtual Machine, work in "mysterious ways" and depending on system configuration (for example, number of processor cores), algorithms will behave vastly different. These scheduling and re-scheduling effects can lead to unexpected starvation.
Here is an example of the naive expectation of how the philosophers would behave:
| Philosopher 1 | Philosopher 2 | Philosopher 3 |
|---|---|---|
| Attempt to pick up left chopstick | Think | Think |
| Acquire left chopstick | Attempt to pick up left chopstick | Think |
| Attempt to pick up right chopstick | Acquire left chopstick | Think |
| Wait for right chopstick | Attempt to pick up right chopstick | Think |
| Wait for right chopstick | Acquire right chopstick | Attempt to pick up left chopstick |
| Wait for right chopstick | Eat | Wait for left chopstick |
| Wait for right chopstick | Eat | Wait for left chopstick |
| Wait for right chopstick | Put down left chopstick | Wait for left chopstick |
Here is a more realistic schedule where the scheduler suspends philosophers 2 and 3 to run other processes:
| Philosopher 1 | Philosopher 2 | Philosopher 3 |
|---|---|---|
| Attempt to pick up left chopstick. | Think | Think |
| Acquire left chopstick. | Think | |
| Attempt to pick up right chopstick | ||
| Acquire right chopstick | ||
| Eat | ||
| Eat | Attempt to pick up left chopstick | Think |
| Put down left chopstick | Wait for left chopstick | Think |
| Put down right chopstick | Wait for left chopstick | Attempt to pick up left chopstick |
It is evident that scheduling can change the behavior significantly, so this is something to bear in mind when implementing solutions. In our case, effects like these could lead to repeated re-acquiring of a chopstick by one philosopher, which could cause starvation of a neighbor. We aim to prevent this based on the computer Science Best-Practice: Anything that can go wrong will go wrong.
Concurrency
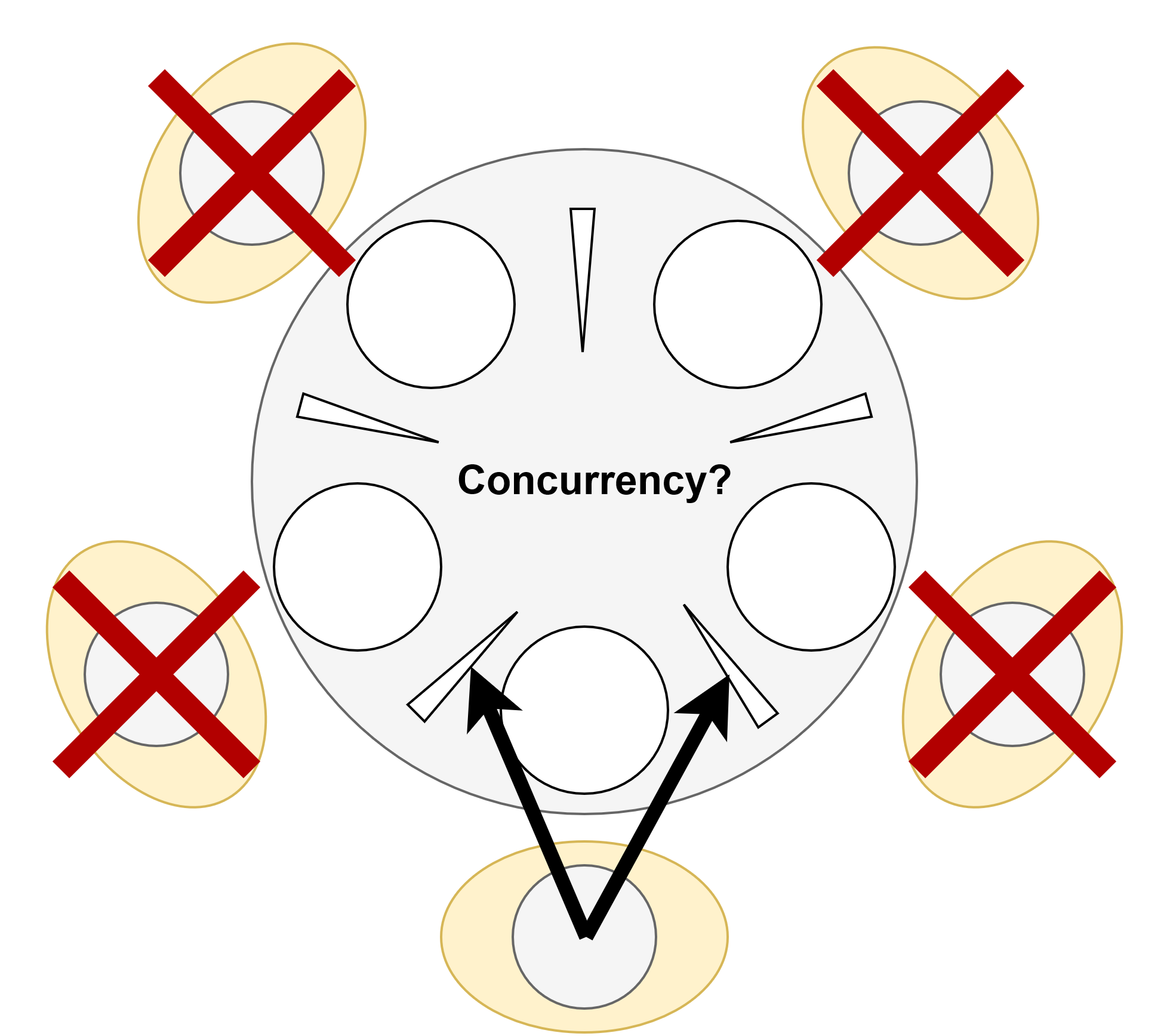
One simple way to prevent deadlocks is to allow only one philosopher to eat at a time. However, this would remove the ability for multiple philosophers to eat at the same time. In our case, concurrency means that multiple philosophers can progress simultaneously without waiting for each other, unless absolutely necessary. Our solution should ideally maintain concurrency while also preventing deadlocks and providing fairness.
To measure concurrency in our system, we introduce the following measure:
- Concurrency: When a simulation is finished, we get a timeline of length l (Total tracked Simulation Time excluding pick-ups/ put-downs). During the simulation we also track the total Eating Time e (The total combined simulation time philosophers spent eating). We then calculate e/l to determine the concurrency within the system during the course of the simulation. With this measure, the bigger the value, the better. For the classic 5-philosopher setup, values close to two are a great result, as this means that, most of the simulation time two philosophers were eating in parallel. (Which is the maximum attainable)
Implementation
We should also consider how challenging the implementation of a solution is when compared to other solutions. Many will be rather simple to implement, while some others will utilize more complex concepts.
Overhead and Scalability
Finally, we want to evaluate algorithms based on the overhead they produce and how scalable they are. Some Solutions use several data structures and synchronization mechanisms that produce additional computational effort. In our case, scalability refers to increasing the number of philosophers at the table. Usually, centralized solutions to the Dining Philosophers are less scalable, since they use a single entity that needs to be accessed in a mutually exclusive manner. Contrary, decentralized and distributed approaches do not suffer from this issue. Real-world definitions of decentralized and distributed algorithms are often fine-grained and complex. For convenience, decentralized approaches are defined to act solely based on locally available information, while distributed approaches employ communication between philosophers.
Limitations
Before exploring solutions, let us discuss the main limitations of the problem. One key limitation is that the rules restrict the maximum concurrency. Under ideal conditions, the maximum number of philosophers who can eat simultaneously is limited to [n/2] for even numbers of n philosophers and ⌊n/2⌋ (integer division) for odd n. The cause for this is that philosopher need two chopsticks to eat, and since each chopstick is shared between two philosophers, at most every other philosopher is allowed to eat at any time. For example, with 5 philosophers, ⌊5/2⌋ equals 2, meaning that at most, two philosophers can eat in parallel.
In real-world systems, access to shared resources often involves more complex dependencies, where multiple processes may share more than two resources, which cannot be replicated using the Dining Philosophers problem without significantly changing its rules. Other constraints, such as the assumed homogeneity of resources (in reality, resources may have different constraints), time constraints (some processes must 'eat' within a specific timeframe), or unexpected unavailability (processes may crash or terminate), are also typically not accounted for. As a result, many solutions we will explore may not directly apply to such real-world systems.
Naive Dining Philosophers Implementation
The following Java-inspired pseudocode demonstrates the implementation principles of a naive solution to the Dining Philosophers problem, leading to deadlocks. The philosophers' actions are logged over time, based on a virtual clock running during the simulation. For simplicity, most of the Java "Boilerplate" (Necessary for Java programs but not useful for understanding of the concept) and some simulation logic for consistency of logs have been omitted. If you are interested in the full implementation of this project, it is available on GitHub here. //link to GitHub
Pseudocode Philosopher class:
class Philosopher extends Thread {
int id;
Chopstick leftChopstick;
Chopstick rightChopstick;
List log;
NaivePhilosopher(int id, Chopstick leftChopstick, Chopstick rightChopstick) {
this.id = id;
this.leftChopstick = leftChopstick;
this.rightChopstick = rightChopstick;
}
@Override
void run() {
while (!terminated()) {
think();
pickUpLeftChopstick();
pickUpRightChopstick();
eat();
putDownLeftChopstick();
putDownRightChopstick();
}
}
void think() {
//calculate sleep time according to distribution
long duration = calculateDuration();
sleep(duration);
Log("[ T ]", VirtualClock.getTime());
}
void pickUpLeftChopstick() {
leftChopstick.pickUp(this);
Log("[PUL]", VirtualClock.getTime());
}
void pickUpRightChopstick() {
rightChopstick.pickUp(this);
Log("[PUR]", VirtualClock.getTime());
}
void eat() {
//calculate sleep time according to distribution
long duration = calculateDuration();
sleep(duration);
Log("[ E ]", VirtualClock.getTime());
}
void putDownLeftChopstick() {
leftChopstick.putDown(this);
Log("[PDL]", VirtualClock.getTime());
}
void putDownRightChopstick() {
rightChopstick.putDown(this);
Log("[PDR]", VirtualClock.getTime());
}
void Log(String event, long timeInstance){
// a log of this style is parsed in the backend to then display the timeline and statistics of the simulation
log.add(event + ":" + timeInstance)
}
}
Pseudocode Chopstick class: The synchronized keyword ensures exclusive access to the pickUp() and putDown() methods. philosophers have to enter a waiting state using the wait() method if the chopstick is currently taken. When another philosopher puts down a chopstick, the waiting philosopher is notified using the notify() method.
class Chopstick {
boolean isAvailable = true;
synchronized boolean pickUp(Philosopher philosopher) {
while (!isAvailable) {
wait();
}
isAvailable = false;
return true;
}
synchronized void putDown(Philosopher philosopher) {
isAvailable = true;
notify();
}
}
Dining Table class: The backbone of the simulation is a virtual clock running during the execution. The philosophers log their Actions according to the current time of the clock.
class Table {
// lists to store chopsticks and philosophers
List chopsticks;
List philosophers;
// constructor to initialize the table with the given number of philosophers
Table(int numPhilosophers) {
chopsticks = new List(numPhilosophers);
philosophers = new List(numPhilosophers);
// initialize chopsticks
for (int i = 0; i < numPhilosophers; i++) {
chopsticks.add(new Chopstick());
}
// initialize philosophers, each with a left and right chopstick
for (int i = 0; i < numPhilosophers; i++) {
Chopstick leftChopstick = chopsticks.get(i);
Chopstick rightChopstick = chopsticks.get((i + 1) % numPhilosophers);
philosophers.add(new Philosopher(leftChopstick, rightChopstick));
}
}
// method to start the dinner: start a thread for each philosopher
void startDinner() {
for (Philosopher philosopher : philosophers) {
new Thread(philosopher).start();
}
}
// method to terminate all philosophers
void stopDinner() {
for (Philosopher philosopher : philosophers) {
philosopher.terminate();
}
}
// method to run the simulation
void execute() {
int simulationTime = 100; // total number of loop iterations
int numPhilosophers = 5; // number of philosophers at the table
Table diningTable = new Table(numPhilosophers);
// start all the philosopher threads
diningTable.startDinner();
// run the simulation using a virtual clock
while (simulationTime > 0) {
// advance clock time
VirtualClock.advanceTime();
// pause for the duration of a timestep (the server-sided simulation uses 5 ms)
timeStep();
// decrement the remaining simulation time
simulationTime--;
}
// stop all the philosopher threads after the simulation time ends
diningTable.stopDinner();
}
}
Naive Dining Philosophers Evaluation
Let us now evaluate the Naive Dining Philosophers, based on the introduced challenges.
| Aspect | Description |
|---|---|
| Deadlocks | The naive implementation frequently leads to deadlocks, especially when the number of philosophers is 5 or lower. Usually, it is harder to come across deadlocks when dealing with larger numbers of philosophers. However, due to factors like changes in the execution environment (Java Virtual Machine or Operating System rescheduling tasks), deadlocks could still occur, especially with longer runtimes. |
| Starvation and Fairness | Due to the possibility of deadlocks, starvation is a fundamental problem in our naive approach. However, letting the philosophers wait for a notification to acquire the chopstick lowers the risk of starvation (when we are lucky and no deadlocks occur), but does not prevent it. Rescheduling or suspension of threads by Operating System or Java VM could allow philosophers to acquire chopsticks repeatedly before their neighbor. The solution to this follows below. |
| Concurrency | The naive Dining Philosophers solution has a limited potential for concurrency (as long as deadlocks do not occur). This is due to the long dependence path in the precedence graph, leading to potential long waiting chains. Simulations frequently have low/no concurrency because of this. |
| Implementation | Implementation of the naive Dining Philosophers is relatively simple with knowledge of concurrent programming. |
| Overhead and Scalability | We will base the performance of solutions on this implementation. Large numbers of philosophers will lead to longer wait chains. |
Improving the naive implementation
In the context of Java, it is important to highlight that most synchronization methods do not provide fairness by default. Many synchronization mechanisms, like the "synchronized" keyword (used to attain an object lock when the function is called), do not maintain a queue of waiting threads. This means that the thread that has waited the longest is not guaranteed to be allowed first. This concept is called Barging and has to be prevented to ensure fairness in our solutions. Luckily, many of the synchronization methods in Java (for example, semaphores) allow so-called fairness parameters that will enable a FIFO (First In First Out) queue on the waiting threads.
For exactly this reason, we utilize fair semaphores to control access to chopsticks in the solutions we explore. This will prevent barging and thus the re-acquiring of chopsticks (contrary to the naive chopstick class). Now, even if the Operating System or Java VM re-schedule or suspend threads, we can guarantee that the longest waiting philosopher will acquire the chopstick first (provided that no deadlock occurs — of course). Note that we introduce an overhead due to the managed FIFO queues.
class Chopstick {
// semaphore controlling access to the chopstick.
Semaphore chopstickSemaphore;
Chopstick(int id) {
// semaphore with one permit and enabled fairness parameter
chopstickSemaphore = new Semaphore(1, true);
}
boolean pickUp(Philosopher philosopher) {
// acquire the semaphore, wait in FIFO queue if not available.
chopstickSemaphore.acquire();
return true;
}
void putDown(Philosopher philosopher) {
// release the semaphore, the longest waiting thread will acquire it.
chopstickSemaphore.release();
}
}
Let us re-evaluate the Naive implementation based on this improvement:
| Aspect | Description |
|---|---|
| Starvation and Fairness | Starvation is still possible due to the possibility of deadlocks, but at least we prevent barging, and therefore the re-acquiring of chopsticks. |
| Overhead and Scalability | We produce additional computational effort due to the FIFO queue on each chopsticks' semaphore. |
Simulation
This website offers a Simulation Page and an Animation Page, both powered by a Java Threads-based backend that is in principle very similar to the pseudocode provided. The Simulation Page allows you to run a simulation with 2–9 philosophers and view the resulting simulation output as timelines, with detailed notes on the simulation settings available on that page. The Animation Page lets you run simulations with five philosophers that are then visually animated, with further details also provided on that page. To see the Naive Dining Philosophers in action, you can try either the Simulation Page or the Animation Page.
Naive Simulation Naive AnimationSolving the Dining Philosophers Problem
The following buttons lead to pages that will introduce you to different approaches to solving the Dining Philosophers problem. They each contain descriptions and evaluations to get insight into their performance, relating to the challenges discussed earlier.
To learn about solutions that focus on organizing the order of the pickups:
Asymmetric/ Resource Hierarchy Solutions (2 Algorithms)To learn about the timeout solution that prevents deadlocks via returning the initially acquired chopstick when the second chopstick is not available within a fixed timeframe:
Timeout Solution (1 Algorithm)To learn about solutions that focus on tokens being passed around by the philosophers:
Circulating Token Solutions (2 Algorithms)To learn about solutions that utilize a central entity to organize the permission to eat or pick up chopsticks:
Waiter Solutions (6 Algorithms)To learn about solutions that utilize semaphores:
Semaphore Solutions (4 Algorithms)To learn about Distributed Solutions:
Distributed Solutions (2 Algorithms)Note on Correct Solutions:
Finding a correct solution to the Dining Philosophers problem is not a trivial task.
Correct solutions must be completely deadlock-free. It is not sufficient for solutions to make deadlock incredibly unlikely.
Performance Tests
If you are interested in the performance tests that were conducted to evaluate algorithm performance in terms of concurrency degree and fairness:
Performance Tests